English to Narayan Translator

Discussion

Figure 2 below shows the underlying geometry of Narayan characters. Each circle, including the circumscribing circle, can be divided into four quarter-arcs. Any Narayan ideographic symbol can be constructed from this geometry by drawing out various quarter-arcs on the smaller circles and on the circumscribing circle. Figure 1 shows how a circle is divided into four equal arcs, each arc comprising a quarter of the circle.

Each quarter-arc in figure 1 may be described mathematically as

Arc(n) = { f(r, n, τ) },  where

f(r, n, τ) = ( f_x(r, n, τ), f_y(r, n, τ) ),   such that

f_x(r, n, τ) = r cos((2(n + τ) - 1)π/4),
f_y(r, n, τ) = r sin((2(n + τ) - 1)π/4),
τ ∈ [0, 1],
n ∈ {0, 1, 2, 3}.

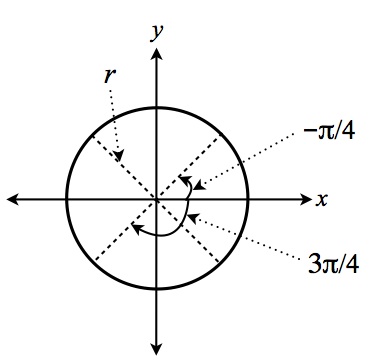
Figure 1. A circle divided up into quarter-arcs.

A Narayan character may be described mathematically as

Arc(m, n) = { ( f_x(r, n, τ) + x_m, f_y(r, n, τ) + y_m ) },   where

x_m = r cos((2m - 1)π/4),
y_m = r sin((2m - 1)π/4),
τ ∈ [0, 1],
m, n ∈ {0, 1, 2, 3}.

which, when combined with the equation for the circumscribing circle,

Arc(k) = { f(2r, k, τ) },  where

τ ∈ [0, 1],
k ∈ {0, 1, 2, 3}.

completely describes the character.


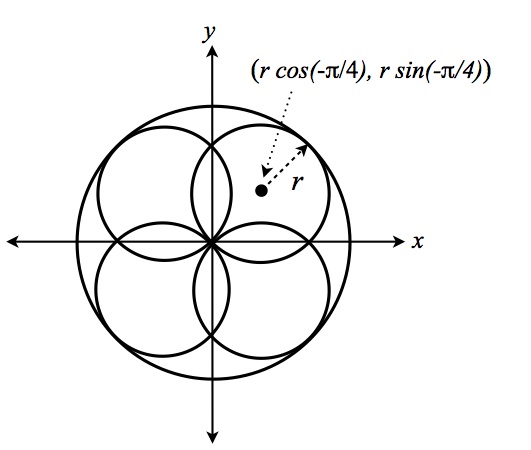
Figure 2. Underlying geometry of a Narayan character.

A Narayan, four word phrase may be constructed by translating each character to its respective cardinal position on a circle of radius 4r/√2. That is, the center of each Narayan character should be located as shown in figure 3. The first character located at the 12:00 position, the second at 3:00, the third at 6:00, and the forth at 9:00.


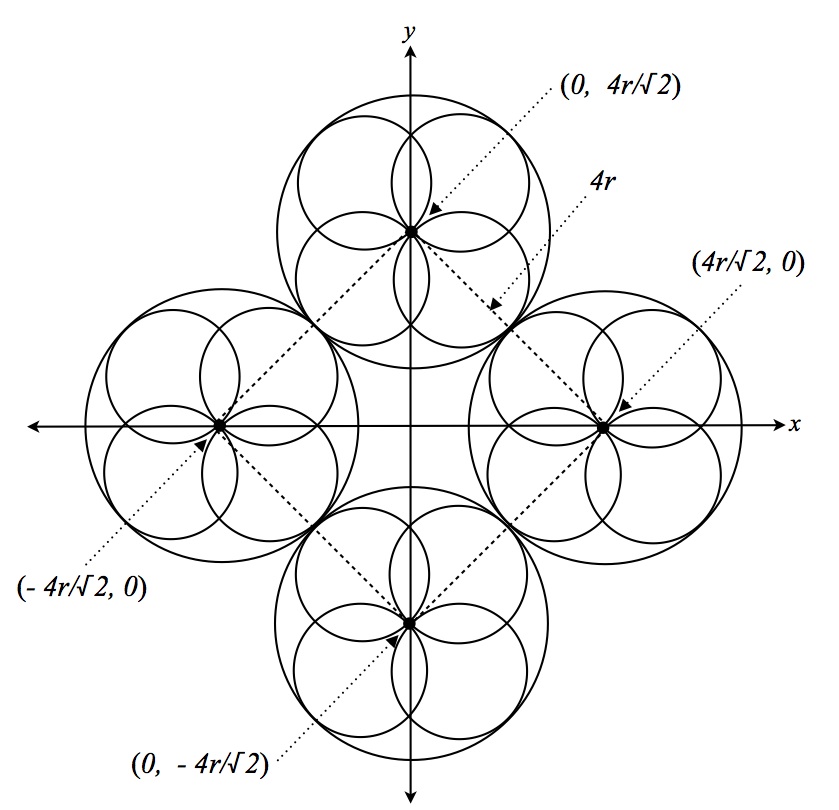
Figure 3. Underlying geometry of a Narayan phrase.

Code Description

The individual quarter-arc segments that make up a Narayan character are stored in a Javascript object that itself contains a set of objects. The property of each object is a Narayan word; the value is a array of integers. The array is organized into pairs of integers as follows. The first integer identifies a specific circle in the underlying geometry of the character

0, the circumscribing circle,
1, the minor circle in the 1:30 position,
2, the minor circle in the 4:30 position,
3, the minor circle in the 7:30 position,
4, the minor circle in the 10:30 position.

The second integer selects a specific quarter-arc on the circle specified by the first integer

0, the quarter-arc centered in the 3:00 position,
1, the quarter-arc centered in the 6:00 position,
2, the quarter-arc centered in the 9:00 position,
3, the quarter-arc centered in the 12:00 position.

Figure 4 shows how pairs of integers are used to specify the quarter-arcs that make up a Narayan character.


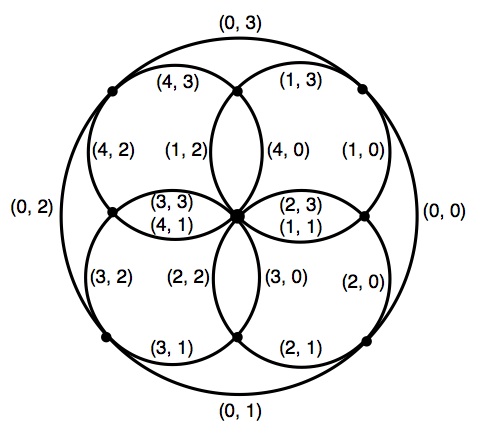
Figure 4. Quarter arcs specified by pairs of integers.

For example, referring to figure 4, in the snippet below the first pair for "Balance" [0,1] identifies the quarter-arc segment in the 6:00 position on the circumscribing circle. The first pair for "Believe" [4,3] identifies the quarter-arc segment in the 12:00 position on the minor circle in the 10:30 position.

var PATTERNS = {
    "": [ ],
    "Balance": [ 0,1, 0,3, 1,0, 1,1, 3,2, 3,3 ],
    "Believe": [ 4,3, 4,2, 4,1, 1,1, 1,0, 0,0, 0,1 ],
    "Change": [ 0,3, 0,2, 3,0, 3,1, 3,2, 3,3, 1,2, 1,1, 4,0, 2,3 ],
    "Chaos": [ 4,2, 0,3, 1,0, 1,2, 2,3, 2,0, 0,1, 3,1 ],
    "Civilization": [ 0,3, 4,2, 4,3, 4,0, 1,2, 1,3, 1,0, 2,2, 2,1,
                      3,0, 3,1 ],
    "Constraint": [ 4,3, 4,2, 4,1, 1,2, 0,1, 0,0, 1,0, 2,0 ],
    .
    .
    .
    };

The code snippet below shows the Javascript function that draws a Narayan phrase on the HTML canvas. Note that xPos and yPos are the x, y coordinates of the center of each word in the phrase. These coordinates correspond to (0, 4r/√2), (4r/√2, 0),
(0, -4r/√2), etc, as shown above in figure 3.

function drawSymbol(sWord, xPos, yPos) {
    /*
     * Description:
     *   Draws a Narayan character, centered at the location
     *   specified by the supplied coordinates.
     * Parameters:
     *   sWord - the Narayan character to draw
     *   xPos, yPos - the coordinates of where to draw the
     *                character
     */
    var i;          // iterating variable
    var mCenter;    // coordinates for center of minor circle
    var piov4;      // a constant equivalent to 45 degrees
    var thetaBegin; // start angle of specified quarter-arc
    var thetaEnd;   // end angle of specified quarter-arc
    var thetaOrg;   // angle of origin of minor circle
    var pattern;    // the array specifying the quarter-arcs

    pattern = PATTERNS[sWord];
    piov4 = Math.PI / 4;

    for(i = 0; i < pattern.length; i++) {
        /*
         * Iterate through pairs of integers in the pattern array
         * that describes the Narayan character specified by sWord.
         * For each pair define the beginning and end points of 
         * quarter-arc specified by the second integer in the pair.
         */
        thetaBegin = (2 * pattern[i + 1] - 1) * piov4;
        thetaEnd = thetaBegin + 2 * piov4;

        if(pattern[i] == 0) {
            /*
             * If the first integer in the pair is 0, then draw on
             * circumscribing circle the quarter-arc specified by the
             * second integer in the pair.
             */
            ctx.beginPath();
            ctx.arc(xPos, yPos, 2 * unitRadius, thetaBegin, thetaEnd);
            ctx.stroke();
            ctx.closePath();
        } else {
            /*
             * If the first integer in the pair specifies a minor circle,
             * then get the rectangular coordinates of the center of the
             * minor circle specified by the first integer.
             */
            thetaOrg = (2 * pattern[i] - 3) * piov4;
            mCenter = rectangularCoordinates(unitRadius, thetaOrg);
            /*
             * Draw the quarter-arc specified by the second integer
             * in the pair.
             */
            ctx.beginPath();
            ctx.arc(mCenter.x + xPos, mCenter.y + yPos,
                    unitRadius, thetaBegin, thetaEnd);
            ctx.stroke();
            ctx.closePath();
        }
        i++;
    }
}

Source Code

You can view the entire source code for this app here.